14. Implementation and Application of K-Nearest Neighbor Regression Algorithm#
14.1. Introduction#
In the experiment of the K-Nearest Neighbor algorithm, we learned the solution idea for using it to solve classification problems. In fact, the K-Nearest Neighbor can also be used for regression analysis and prediction. In this challenge, you will complete the transformation of the K-Nearest Neighbor algorithm and apply it to regression analysis.
14.2. Key Points#
-
Introduction to K-Nearest Neighbor Regression
-
Implementation of K-Nearest Neighbor Regression
14.3. Content Review#
Recall what we learned in the K-Nearest Neighbor experiment. When using the K-Nearest Neighbor algorithm to complete a classification task, the steps required are:
-
Data Preparation: Through data cleaning and data processing, organize each piece of data into a vector.
-
Calculate Distance: Calculate the distance between the test data and the training data.
-
Find Neighbors: Find the K training data samples that are closest to the test data.
-
Decision Classification: According to the decision rule, obtain the class of the test data from the K neighbors.
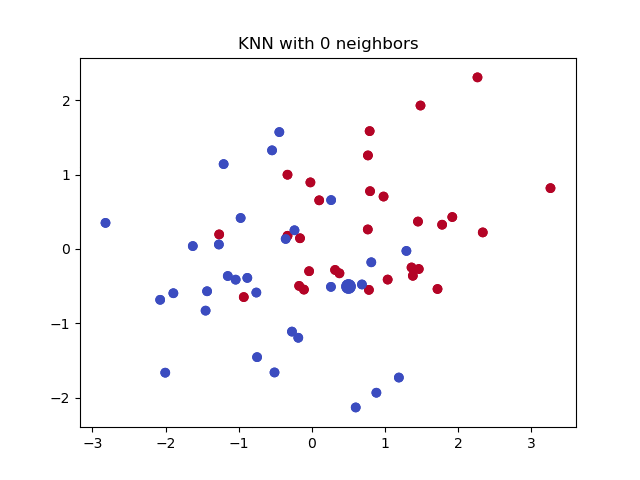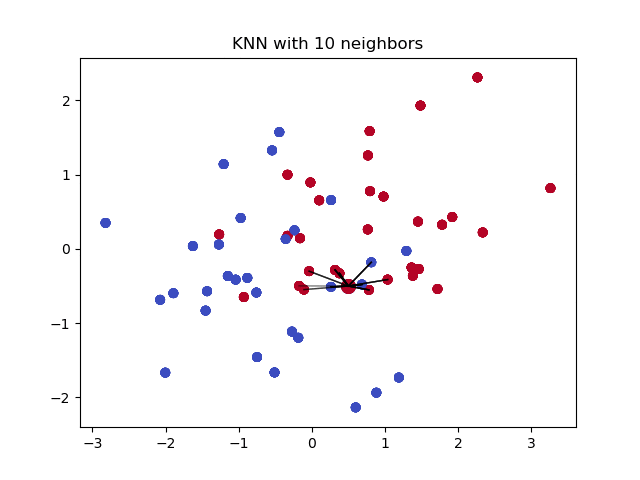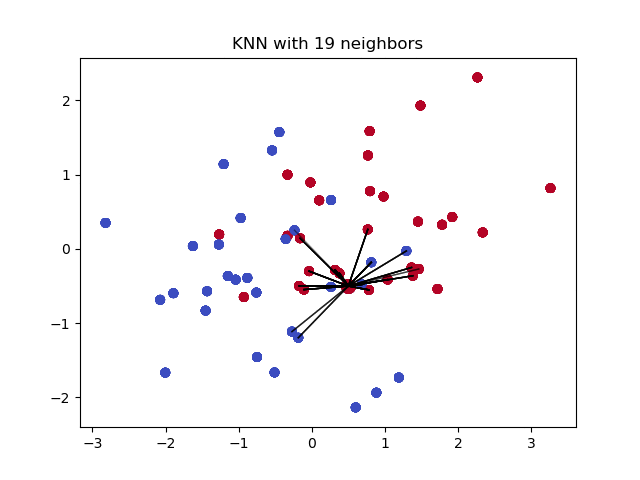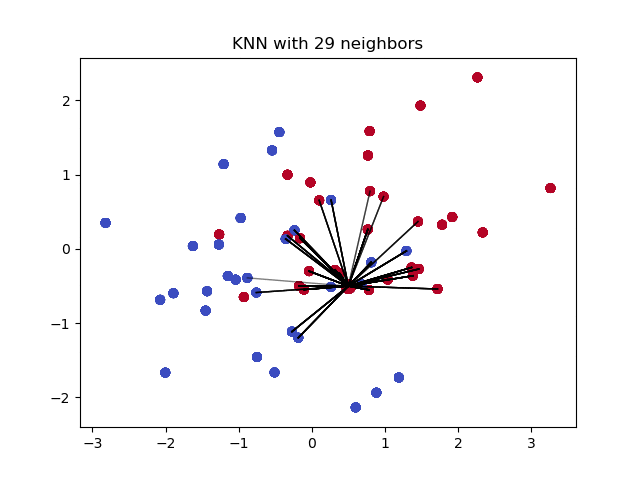
Among them, “Decision Classification” is the key step in determining the category of unknown samples. Then, when we apply the K-Nearest Neighbor algorithm to regression prediction, we actually only need to modify this step to a process suitable for regression problems.
-
Classification Problem: Based on the classes of the K neighbors, obtain the class of the unknown sample through majority voting.
-
Regression Problem: Based on the target values of the K neighbors, calculate the average value to obtain the predicted value of the unknown sample.
The illustration of the K-Nearest Neighbor regression algorithm is as follows:
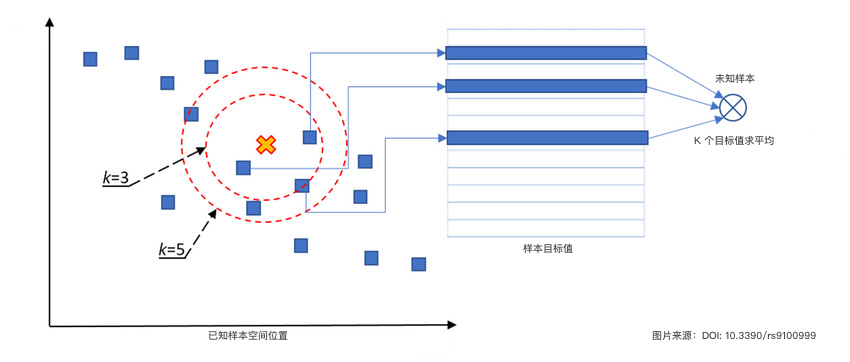
Next, you need to implement the K-Nearest Neighbor regression algorithm based on the above illustration and description, and verify it with sample data.
Exercise 14.1
Challenge: Implement the K-Nearest Neighbor regression algorithm based on the above illustration and description.
Specification: Use the Euclidean distance formula for distance calculation, and some code can be referred to the experimental content.
def knn_regression(train_data, train_labels, test_data, k):
"""
参数:
train_data -- 训练数据特征 numpy.ndarray.2d
train_labels -- 训练数据目标 numpy.ndarray.1d
test_data -- 测试数据特征 numpy.ndarray.2d
k -- k 值
返回:
test_labels -- 测试数据目标 numpy.ndarray.1d
"""
### 代码开始 ### (≈ 10 行代码)
test_labels = None
### 代码结束 ###
return test_labels
Solution to Exercise 14.1
def knn_regression(train_data, train_labels, test_data, k):
"""
Parameters:
train_data -- Training data features numpy.ndarray.2d
train_labels -- Training data targets numpy.ndarray.1d
test_data -- Test data features numpy.ndarray.2d
k -- The value of k
Returns:
test_labels -- Training data targets numpy.ndarray.1d
"""
### Start of code ### (≈ 10 lines of code)
test_labels = np.array([]) # Create an empty array to store the prediction results
for X_test in test_data:
distances = np.array([])
for each_X in train_data: # Calculate data similarity using Euclidean distance
d = np.sqrt(np.sum(np.square(X_test - each_X)))
distances = np.append(distances, d)
sorted_distance_index = distances.argsort() # Get the indices sorted by distance
k_labels = train_labels[sorted_distance_index[:k]]
y_test = np.mean(k_labels)
test_labels = np.append(test_labels, y_test)
### End of code ###
return test_labels
Next, we provide a set of test data.
import numpy as np
# 训练样本特征
train_data = np.array(
[[1, 1], [2, 2], [3, 3], [4, 4], [5, 5], [6, 6], [7, 7], [8, 8], [9, 9], [10, 10]]
)
# 训练样本目标值
train_labels = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
Run the test
# 测试样本特征
test_data = np.array([[1.2, 1.3], [3.7, 3.5], [5.5, 6.2], [7.1, 7.9]])
# 测试样本目标值
knn_regression(train_data, train_labels, test_data, k=3)
Expected output
array([2., 4., 6., 7.])
